How to Teach Multiplying Fractions with Pattern Blocks
My first year teaching, I inherited approximately 1,000,000 math manipulatives - plastic tubs full of pattern blocks, fraction tiles, play money, counters, geoboards, measuring tapes, and thousands of 1-inch plastic tiles. Young and eager, I jumped in headfirst with the manipulatives. My students used nearly every manipulative under the sun… with the exception of the pattern blocks.
“What in the world can students do with pattern blocks in fourth and fifth grade?” I wondered.
If only I’d known what an incredible tool they are for teaching fractions, those pattern blocks would’ve gotten a lot more use (and my students would’ve understood fractions a lot better!).
Pattern blocks are now my absolute favorite way to teach all fraction concepts. What makes them so powerful is that students have to rely on their understanding of fractions as a relationship of a part of a whole. Also, having the different shapes helps students really see how certain pieces fit into others. Since there are no fraction labels on the pieces, the possibilities are endless in how you use pattern blocks!
While I now use pattern blocks to teach all fraction concepts, my favorite fraction concept to teach with pattern blocks is multiplying fractions. Since the algorithm for fraction multiplication looks so easy, it’s tempting to hand students the “shortcut” and skip out on building conceptual understanding.
But building conceptual understanding is SO important, especially with fractions!
Multiplying fractions can be a difficult concept to make hands-on, but pattern blocks make it simple (and so much fun!). Let’s walk through some example problems so that you can bring this powerful activity to your classroom!
watch the video...
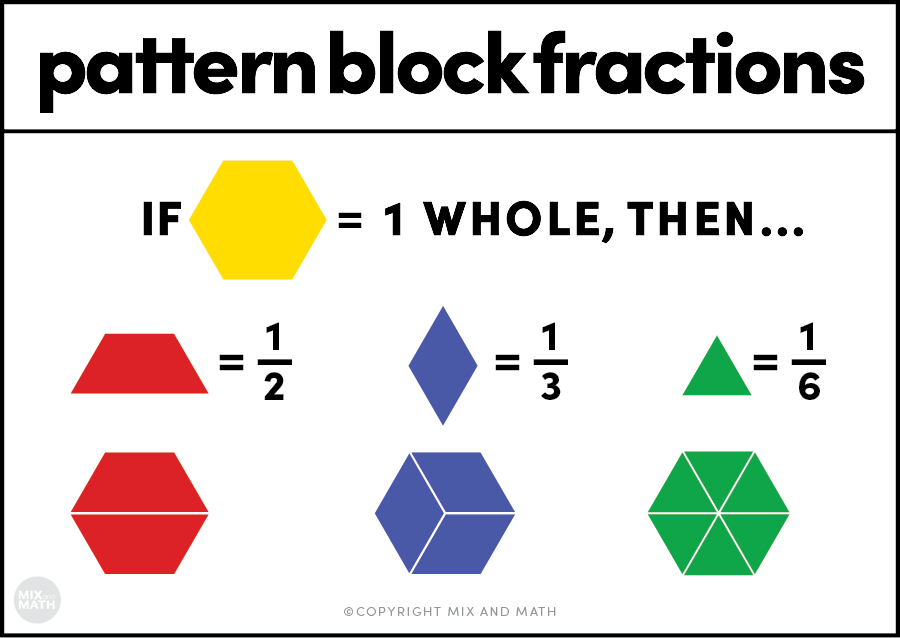
Before we get into how to teach multiplying fractions with pattern blocks, make sure you (and your students!) are clear about what fraction each pattern block represents. While you can make any piece represent one whole, most often I use the hexagon as one whole.
The graphic below shows the value of each pattern block piece when the hexagon is one whole.
An important thing to note about pattern blocks is that you will be limited to denominators of halves, thirds, and sixths for the problems you create! They do make an add-on pattern block set for fourths and twelfths if you want to supplement the blocks you already have!
Now that you know the value of each pattern block, let’s dive into how students can use pattern blocks to model all different types of fraction and mixed number multiplication problems.
Multiple Groups/Equal Groups Problems
There’s a clear progression to how fraction multiplication problems should build. The first step in the progression is multiplication as multiple groups or equal groups.
Viewing multiplication as multiple groups is relatively easy for students to understand because it follows the same line of thinking as whole number multiplication. It’s not a big leap for students to go from understanding 2 groups of 3 (2 x 3) to understanding 2 groups of ⅔ (2 x ⅔).
However, it will take plenty of hands-on opportunities before students discover the algorithm for multiplying a whole number by a fraction. (And they will see it! Trust the process and don’t push the algorithm before students are ready!)
Here’s an example of a multiple groups problem:
Stella’s dog ate 3 bags of dog food last week. If each bag contained ⅔ pounds of dog food, how many pounds of food did Stella’s dog eat?
On the math mat, students would model three groups of ⅔. They might call it 6/3, or rearrange the pieces into wholes to see that the answer is two wholes. Stella’s dog ate 2 pounds of dog food last week.
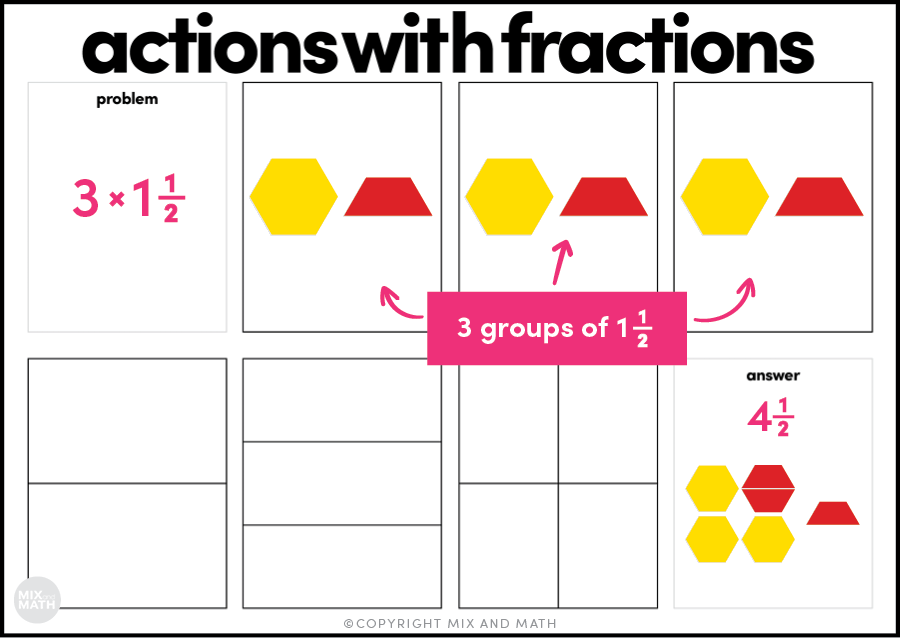
Multiple groups problems can also include mixed numbers as the multiplicand, like 3 groups of 1 ½. As long as the multiplier (the number of groups) is a whole number, it would be modeled similarly to how the last problem was modeled. Take a look at the graphic below to see how you would model 3 x 1 ½ with pattern blocks.
For fourth grade, most state standards stop here (of course, check your own standards just to be sure!). For fifth grade, however, they need to understand another type of fraction multiplication problem.
Partial Groups Problems
The goal of this step in the multiplication progression is for students to start looking at multiplication as scaling, specifically resizing to find part of a group. This can feel like a big shift from what students think they know about multiplication which is, “multiplication makes numbers bigger!”
It is at this point that they learn that multiplication can result in a smaller product, which means we absolutely have to give students the opportunity to model this concept, or else this can feel incredibly confusing!
Part of a Whole
The first type of partial groups problem is finding part of a whole.
Let’s go back to our real-world situation with dog food to see what this looks like.
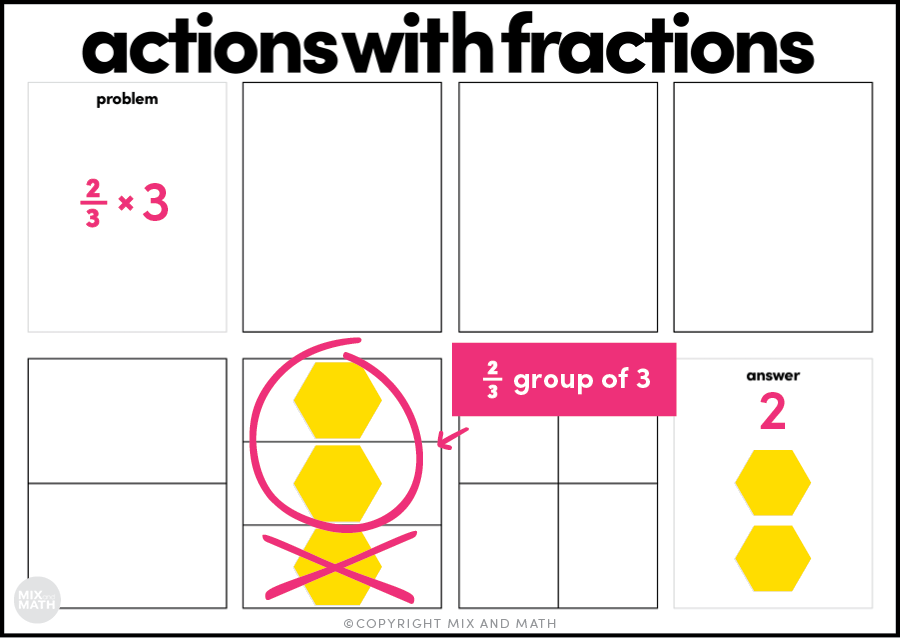
Stella’s dog ate ⅔ of a bag of dog food last week. If each bag contained 3 pounds of dog food, how many pounds of food did Stella’s dog eat?
While the equation for this problem is the same as the previous problem (⅔ x 3 vs. 3 x ⅔), the action of modeling this out feels very different. In this case, students must understand that they’re finding ⅔ of a group of 3. Another way to say this is ⅔ of 3.
Students need lots of opportunities with both types of problems to recognize them both as multiplication!
To model ⅔ of 3, students would start with 3 wholes and then they would need to figure out how to split it into thirds (or three equal groups). They’d see that they need to put one whole into each of the thirds. Since we want to know what ⅔ of 3 is, we know the answer will include two of the thirds which is two wholes because each third has one whole in it. See the graphic below for how to model this.
Let’s take this partial groups type of thinking a little further by looking at how to model a fraction by a fraction.
Part of a Part
The next type of partial group problem is part of a part. Again, let’s use our real-world context to help us understand what this actually means.
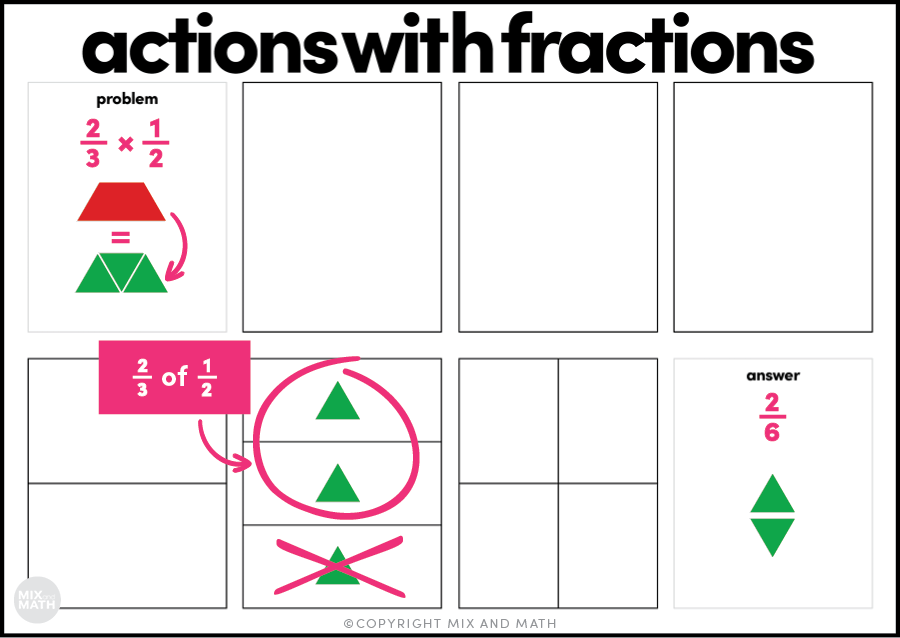
Stella’s dog ate ⅔ of a bag of dog food. If each bag contains ½ a pound of dog food, how many pounds of food did Stella’s dog eat?
Instead of finding part of a group, this situation calls for finding part of another part… What is ⅔ of the ½ a pound of food? In order to model this, they will need to do a bit of exchanging to help them act this out. We know that a trapezoid (1 half) is equivalent to 3 triangles (or 3 sixths), which means students can trade out the trapezoid for 3 triangles. This will help us as we try to figure out what ⅔ of half is.
Look at the graphic below to see how a student would put one-sixth into each of the third sections to help them figure out that 2 thirds of half is two-sixths.
The very last step in this progression for multiplying fractions is the fun part. Now students are really challenged to apply what they’ve learned!
Combining Multiple and Partial Groups
The final step in the progression of truly understanding fraction multiplication is a combination of both multiple groups and partial groups. This means that the multiplier (the number of groups) is a mixed number, forcing students to think about an equal number of groups and part of a group or part.
Let’s look at a couple of examples below of what this actually looks like!
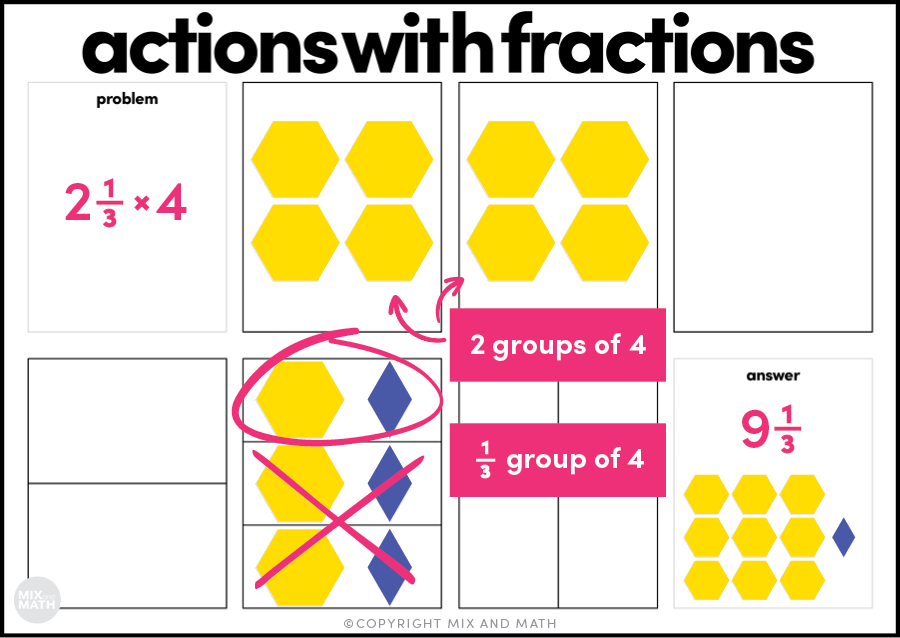
Stella’s dog ate 2 ⅓ bags of dog food last month. If each bag holds 4 pounds of dog food, how many pounds of food did Stella’s dog eat?
In this situation, Stella’s dog ate 2 bags of food (2 x 4 pounds—multiple groups) and ⅓ of a bag of food (⅓ x 4 pounds—partial groups). Students must combine their understanding of both types of fraction multiplication to successfully solve this problem.
This problem is modeled in the graphic below.
After combining 2 groups of 4 and ⅓ of 4, you’ll see that Stella’s dog ate a total of 9 ⅓ pounds of dog food.
Let’s take a look at another problem where the multiplicand (what is being multiplied) is a fraction!
Stella’s dog ate 2 ⅓ bags of dog food. If each bag contained ½ a pound of dog food, how many pounds of food did Stella’s dog eat?
In this situation, Stella’s dog ate 2 groups of ½ pound (multiple groups) and ⅓ of ½ (part of a part). In the graphic below you can see that when it is all combined, Stella’s dog ate 1 ⅙ pounds of dog food.
In the final problem that we’ll look at in this post, students are solving a fraction multiplication problem that involves a mixed number by a mixed number.
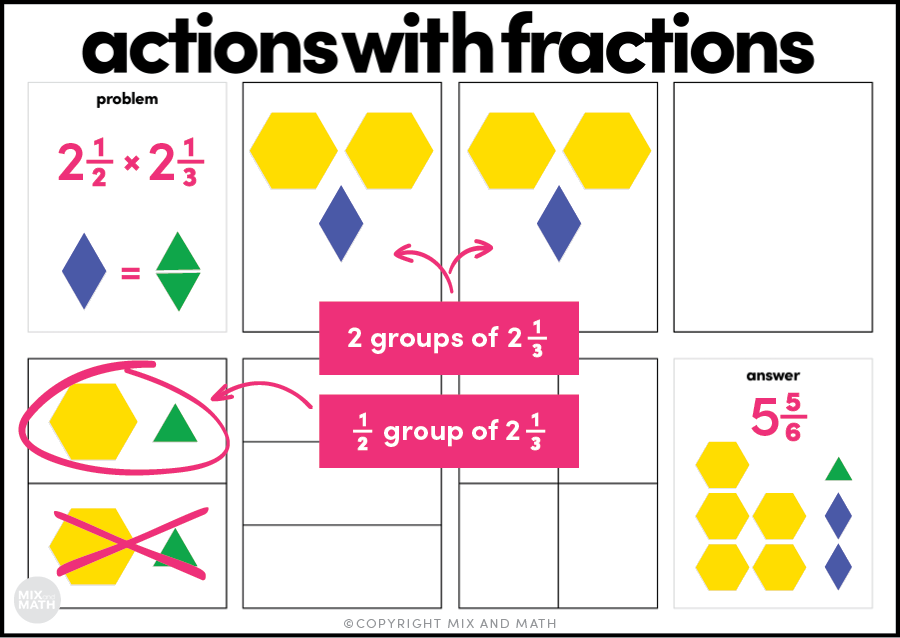
Stella’s dog ate 2 ½ bags of dog food last week. If each bag contained 2 ⅓ pounds of dog food, how many pounds of food did Stella’s dog eat?
In this problem, there are 2 ½ groups of 2 ⅓, which is 2 full groups of 2 ⅓ (multiple groups) and ½ of a group of 2 ⅓ (partial groups). Since students have hopefully had so much experience with multiple groups and partial groups prior to this problem, this process is absolutely doable for students (though it may stretch their thinking!).
I hope you now see what a game-changer pattern blocks are for multiplying fractions. While it might seem inefficient to have students spend all this time modeling out fraction multiplication, the groundwork will pay off in the end when students truly understand the actions and meaning behind the algorithms!
If you’re like I was and you don’t know what to do with pattern blocks in fourth and fifth grade, it’s time to dust them off. You’re missing out on one of the most powerful tools for building students’ understanding of fractions!
Want to use this activity with your students? Be sure to download the FREE math mat below!